SNR: Sub-Network Routing for Flexible Parameter Sharing in Multi-Task Learning

Introduction

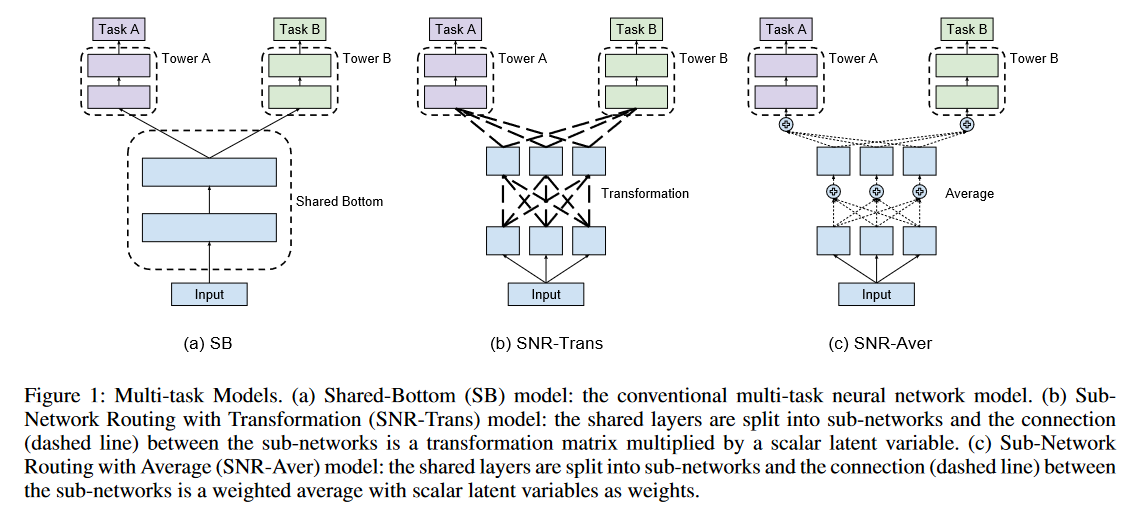
这篇文章主要是针对Shared Botton（SB）形式的多任务学习进行改进

SB的问题在于，当不同的任务之间相关性比较弱的时候，模型的表达能力会急剧恶化。权宜之计是人工的进行任务的筛选，让更相关的任务共享更多模型结构，反之则减少共享。但是这样的方法难以拓展（Scalable）

为了解决多任务的参数共享问题，作者提出了可变的参数共享的网络

与门结构类似，但不同：

• 门结构不够灵活，如果足够灵活需要牺牲计算成本
• 作者方法可以实现灵活的参数共享并保持计算优势

Method

具体而言，作者通过控制网络之间的连接进行权重的灵活控制

简单来说，对于每个网络的权重都有对应的weight进行加权，这个weight权重，作者称之为coding variables

在serving时，serving code是一个确定的估计值，因此计算量也得到了降低

重点关注SNR-Trans这个结构。本质上，模型的学习入下公式，除了权重W，还要学习模型的连接权重（conding variable）z。

\[\begin{bmatrix} \boldsymbol{v_{1}}\\ \boldsymbol{v_{2}} \end{bmatrix} = \begin{bmatrix} z_{11}\boldsymbol{W_{11}}&z_{12}\boldsymbol{W_{12}}&z_{13}\boldsymbol{W_{13}}\\ z_{21}\boldsymbol{W_{21}}&z_{22}\boldsymbol{W_{22}}&z_{23}\boldsymbol{W_{23}} \end{bmatrix} \begin{bmatrix} \boldsymbol{u_{1}}\\ \boldsymbol{u_{2}}\\ \boldsymbol{u_{3}} \end{bmatrix}\]

公式代表一个输入维度为3，输出为2的模型，按照Figure1三个低层三个高层模型的结构，其公式可以变换为。

\[\begin{bmatrix} \boldsymbol{v_{1}}\\ \boldsymbol{v_{2}}\\ \boldsymbol{v_{3}} \end{bmatrix} = \begin{bmatrix} z_{11}\boldsymbol{W_{11}}&z_{12}\boldsymbol{W_{12}}&z_{13}\boldsymbol{W_{13}}\\ z_{21}\boldsymbol{W_{21}}&z_{22}\boldsymbol{W_{22}}&z_{23}\boldsymbol{W_{23}}\\ z_{31}\boldsymbol{W_{31}}&z_{32}\boldsymbol{W_{32}}&z_{33}\boldsymbol{W_{33}} \end{bmatrix} \begin{bmatrix} \boldsymbol{u_{1}}\\\boldsymbol{u_{2}}\\\boldsymbol{u_{3}}\end{bmatrix}\]

在图像上， $ z$ 就可以理解为虚线的部分，代表每个连接的权重。

参考已有的工作，这里的 $ z$ 是通过一个0-1的均匀分布学习得到的，其公式化的表示为：

\[u\sim U(0,1),s=\mathrm{sigmoid}((\log(u)-\log(1-u)+\log(\alpha)/\beta)\\\bar{s}=s(\zeta-\gamma)+\gamma,z=\min(1,\max(\bar{s},0)),\]

在代码上，根据已有的开源代码¹，可以更好的理解模型的forward过程

class Transform_layer(nn.Module):
    def __init__(self, input_size, output_size, config):
        super(Transform_layer, self).__init__()
        self.alpha = torch.nn.Parameter(torch.rand((1,), device=config.device), requires_grad=True)
        self.beta = 0.9
        self.gamma = -0.1
        self.eplison = 2

        w = torch.empty(input_size, config.num_experts,output_size, device=config.device)
        self.u = torch.nn.Parameter(torch.nn.init.uniform_(w, 0, 1),
                                    requires_grad=True)

        w = torch.empty(input_size,config.num_experts, output_size, device=config.device)
        self.w_params = torch.nn.Parameter(torch.nn.init.xavier_normal_(w),
                                           requires_grad=True)

    def forward(self, x):
        self.s = torch.sigmoid(torch.log(self.u) - torch.log(1 - self.u) + torch.log(self.alpha) / self.beta)
        self.s_ = self.s * (self.eplison - self.gamma) + self.gamma

        self.z_params = (self.s_ > 0).float() * self.s_
        self.z_params = (self.z_params > 1).float() + (self.z_params <= 1).float() * self.z_params

        output = self.z_params * self.w_params
        output = torch.einsum('ab,bnc -> anc', x, output)
        return output

Serving 和Training 的不同

作者参考已有的一篇文献²，在serving阶段，z 的计算变为

\[\hat{\boldsymbol{z}}=\min(1,\max(0,\mathrm{sigmoid}(\log(\boldsymbol{\alpha}))(\zeta-\gamma)+\gamma)).\]

这样仅使用了 $ \alpha$ 而没有使用维度更高的参数 $ u$ ，也进一步降低了计算成本（其实如果直接将 $z W$ 的结果进行保存，也是同样节省了重复计算的复杂度）

这里可以将serving和training的coding variable进行变换，主要还是因为  $ u$ 符合0-1的均值分布，在作者引用参考文献了，论证了如果这样的 $ u$ 和 $\alpha$  一起学习，最后得到的 $\alpha$ 可以作为 deterministic estimator直接抛弃 $ u$ 使用。

正则化

正则化可以产生稀疏的模型结构，能够降低模型的存储空间（0值可以压缩），还能够降低计算成本（在深度学习框架中会优化稀疏矩阵相乘）

作者引入L0正则化，其公式表达为

\[\boldsymbol{E}_{\boldsymbol{z}\sim p(\boldsymbol{z};\boldsymbol{\pi})}||\boldsymbol{z}||_0=\sum_{i=1}^{|\boldsymbol{z}|}1-Q(s_i<0;\phi_i).\]

如代码¹中的

s1 = self.trans1.s_
s2 = self.trans2.s_ # trans1/2都是Transform_layer，则s_


s1_prob = 1 - ((s1 < 0).sum(dim=-1) / s1.size(1))
s2_prob = 1 - ((s2 < 0).sum(dim=-1) / s2.size(1))

regul = self.lamdba * (s1_prob.sum() + s2_prob.sum())

在训练时，反向传播计算的损失，包括任务的损失加上正则项两项

Result

在YouTuBe8M多标签分类任务上进行评估，对比SB，MMoE提升明显

有趣一些的是关于正则化的实验结果，如下图，可以发现其实不加正则化(Dense)，它的效果其实在模型规模较大的时候，效果表现是更好的，但是在较低的参数量下则结果相反

[image]

个人总结

不太理解Serving阶段的简化操作，需要去了解参考文献的推理过程

SNR在实践中还是非常有效的方法，比较适用于高层（专家层）之后。其实本质上 $ z $ 就是一种剪枝，而且这种剪枝还是没有输入的，是在训练时增加了模型的复杂度。或许优化成一个带有输入的pruner，会更加灵活，当然也提高了模型的复杂度。

参考资料

1. https://github.com/tomtang110/Multitask/blob/master/Models/snr_trans.py ↩︎ ↩︎²

2. Louizos C, Welling M, Kingma D P. Learning sparse neural networks through $ L_0 $ regularization[J]. arXiv preprint arXiv:1712.01312, 2017. ↩︎