Progressive Layered Extraction (PLE): A Novel Multi-Task Learning (MTL) Model for Personalized Recommendations
Alibaba Group 2020 RecSys | 用渐进式分层提取语义信息,解决推荐系统中的多任务问题
用渐进式分层提取语义信息,解决推荐系统中的多任务问题
文章的突出贡献就是从实验的角度,分析了很多已有方法,并归纳得出了一些重要的insight,可以当成一篇有证明的综述阅读
跷跷板与负迁移现象
在现实世界的推荐系统中,多个任务之间可能是稀疏相关甚至矛盾的,因此用一个模型完成多个任务可能会带来负迁移的表现退化。已有的一些多任务工作尝试解决负迁移问题(例如Stitch, Sluic Network和MMoE),但是没有解决了跷跷板现象
跷跷板 seesaw:一个任务表现的提升牺牲了另一个任务
负迁移 negative transfer:多个任务的信息共享导致某些任务表现更差
Contributions
- 通过大量的实验发现了跷跷板现象,具体而言是多任务的模型提升了一些任务的表现,但是某些任务上不如单一任务的模型
- 提出了渐进式分层提取语义的学习结构,可以同时解决跷跷板和负迁移现象
跷跷板现象的实验
对于视频推荐上,作者定义了推荐的融分公式:
\[score=p_{VTR}^{w_{VTR}}\times p_{VCR}^{w_{VCR}}\times p_{SHR}^{w_{SHR}}\times\cdots\times p_{CMR}^{w_{CMR}}\times f(video len)\]其中 $w$ 为每个分数项的稀疏,最后的 $f(videoLen)$ 是关于视频长度的非线性变换(其实就是拟合用户对于视频长度的偏好)
在公式中的多个任务中,作者以完播率(View Completion Rate, VCR) 和浏览率 (View-Through Rate)两个任务举例,认为两个任务有复杂的内部联系,会产生跷跷板现象。给出的原因:VCR是回归任务而VTR是分类任务(当用户观看时间超过某个阈值,则浏览记录+1),首先VTR受到“用户观看”和“停留”同时影响,用户观看这个动作在WIFI的自动播放场景和没有WIFI的场景下的分布是很复杂的。这种复杂与强相关带来了跷跷板现象
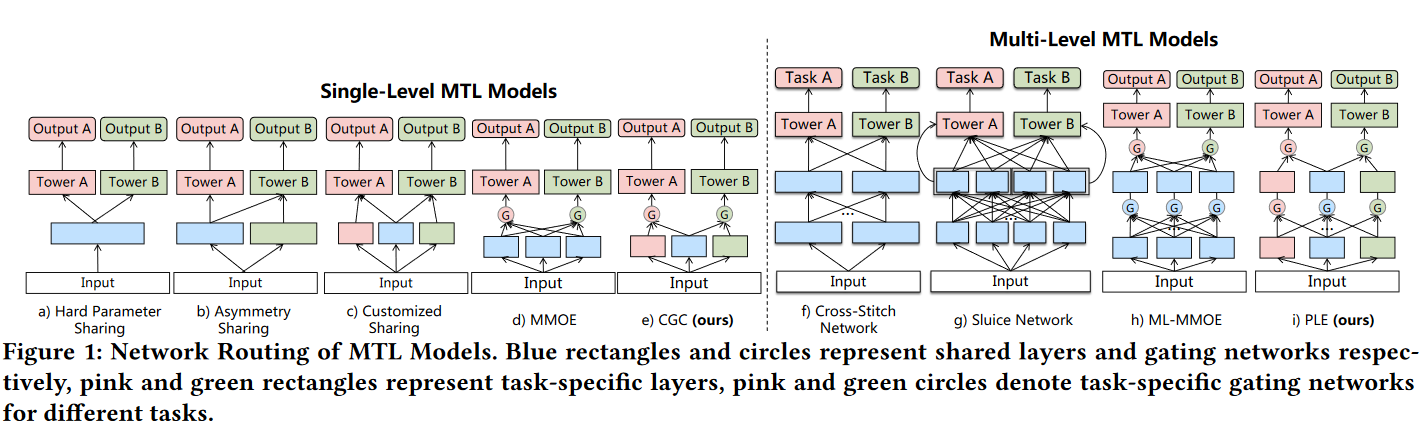
作者将当前的多任务模型区分为单层(MMoE)的和多层(Stitch和Sluic Network)的,并额外提出了单层的多任务融合方法:不对称共享(b)和特定共享(c)
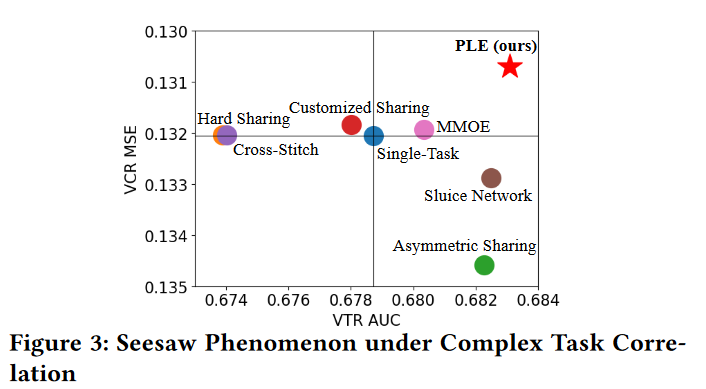
得到的实验结果如图3
如果视Single-Task为坐标原点,在第二和第四象限的方法就是发生了跷跷板现象,在第三象限其实就代表负迁移现象。MMoE在VCR任务上只提高了0.0001
这个实验很好的证明了作者的观点:已有方法解决了负迁移,但是忽略了跷跷板
作者认为类似于VCR和VTR的关系在推荐系统中是广泛的,例如CTR和CVR
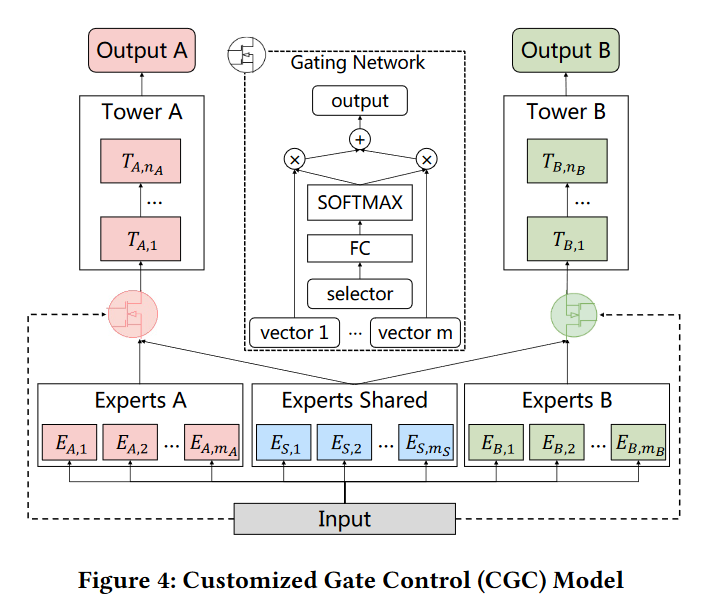
Customized Gate Control (CGC)
特定门单元是PLE的基本结构,后续也被多个模型所使用。主要思想是多个模型由共享专家系统(Experts Shared)和任务特定的专家系统(几个任务就有几个专家系统)构成
与特定共享(Figure 1c)的区别 **: 特定共享是将共享专家和特定任务专家的输出进行concatenation输入到塔中,而CGC是将输出经过门网络再输入进塔中,门网络也是任务特定的**
输入为Embedding的专家系统输出的concatenation:
\[S^k(x)=[E_{(k,1)}^T,E_{(k,2)}^T,\ldots,E_{(k,m_k)}^T,E_{(s,1)}^T,E_{(s,2)}^T,\ldots,E_{(s,m_s)}^T]^T\]对于第k各任务而言,其门网络 $g^k$ ,参数为$W_g^k$ 可以定义为:
\[w^k(x)=\mathrm{Softmax}(W_g^kx),\\ g^k(x)=w^k(x)S^k(x)\]注意,门网络存在跳跃连接。由塔 $t^k$ 可以定义最终的输出:
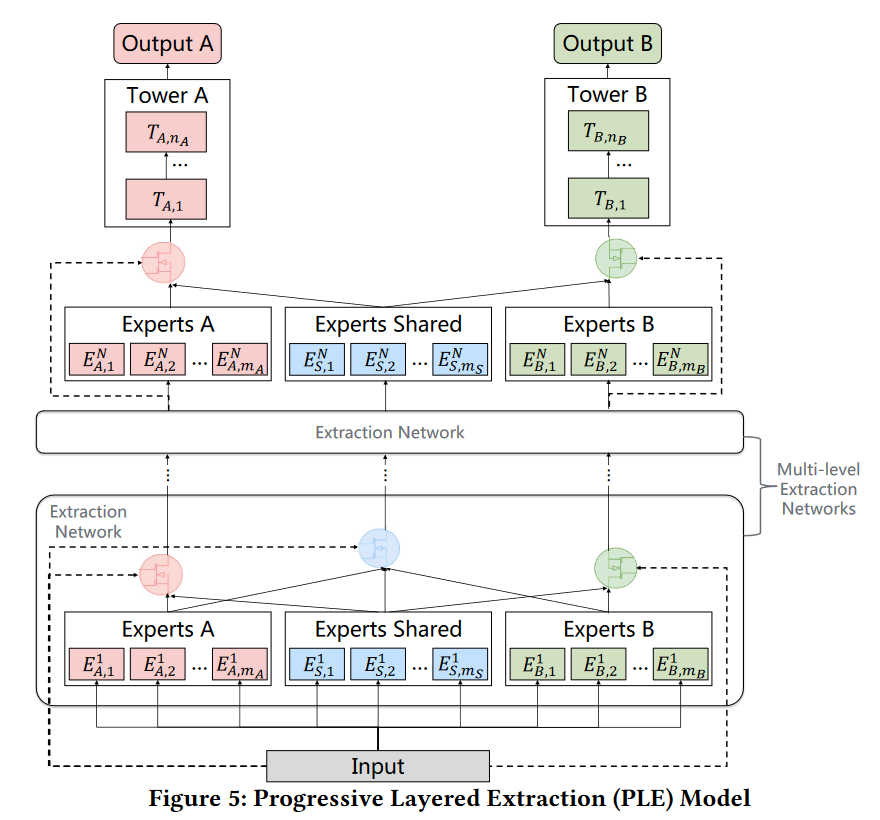
\[y^k(x)=t^k(g^k(x)),\]渐进式层次提取
与CGC的不同
- 除最后一层,门的输入由当前任务特定的模型和共享模型变为所有模型
- 公式中的x为输入的表征,在PLE中,为上一层的结果进行concatenation
训练细节
归一化的任务损失
对于K个任务的模型,其训练的损失函数为各个任务的损失和
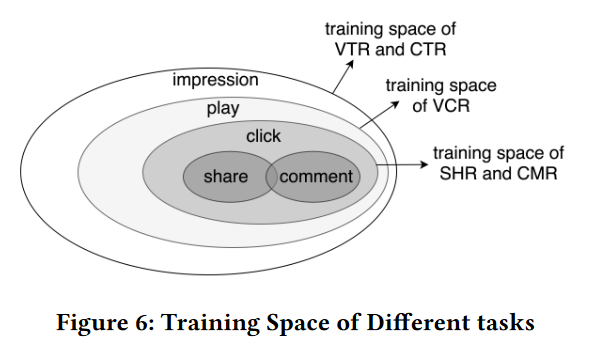
\[L(\theta_1,\ldots,\theta_K,\theta_s)=\sum_{k=1}^K\omega_kL_k(\theta_k,\theta_s),\]但是,由于用户行为是序列的,所以多个任务的样本是不一致的,如图6所示
因此,在此基础上,需要调整每个任务的损失计算方法,作者通过归一化损失来控制
\[L_k(\theta_k,\theta_s)=\frac{1}{\sum_i\delta_k^i}\sum_i\delta_k^iloss_k(\hat{y}_k^i(\theta_k,\theta_s),y_k^i)\]其中$ \delta_{k}^{i}\in{0,1}$ 代表该样本 $i$ 在不在任务 $k$ 中,例如一个用户(输入数据)点击并进行分享,他就会在浏览任务中、操作任务中、点击任务和分享任务中计数,但不会在评论的任务中计算loss。在模型上,这个数据会forward所有的模型,但是只有在任务中的才会计算损失
迭代中调整任务 k 的权重 w
作者的实验发现,不同的任务由不同的训练阶段。而多任务中各个任务的系数又是敏感的,所以作者提出了用一个系数 $\gamma_k$ 来更新损失是系数
\[\omega_k^{(t)}=\omega_{k,0}\times\gamma_k^t,\]公式中的 $w_k^{(t)},\gamma_k^t$ 中的 $t$ 含义不同,分别代表的是第 $t$ 轮epoch的系数,以及 $\gamma$ 的 $t$ 次方
实验
数据集采用腾讯新闻自己的数据集,前七天作为训练集,第8天作为测试集。
对于所有的模型,均采用三层全连接网络,和ReLU激活,隐藏层的大小为[256,128,64],对比方法在图1很好的展示了,所有的多层方法层数保持一致(具体没说)
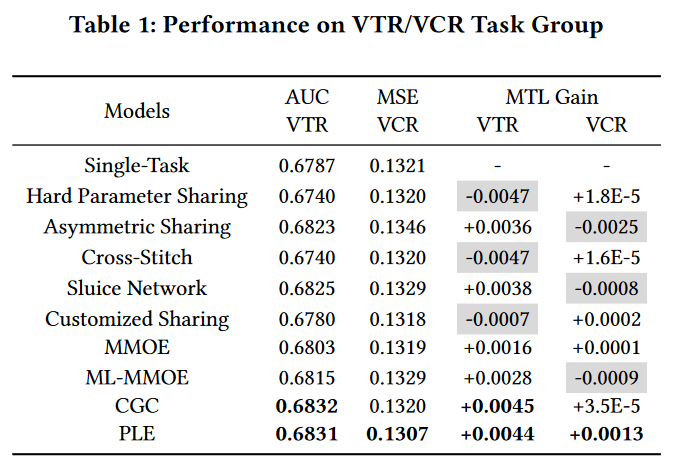
Metric用AUC和MSE分别评估VTR和VCR,作者还提出了一个MTL Gain,其实就是和single-Task的比较值,当两个值出现一正一负,就说明出现了跷跷板现象。
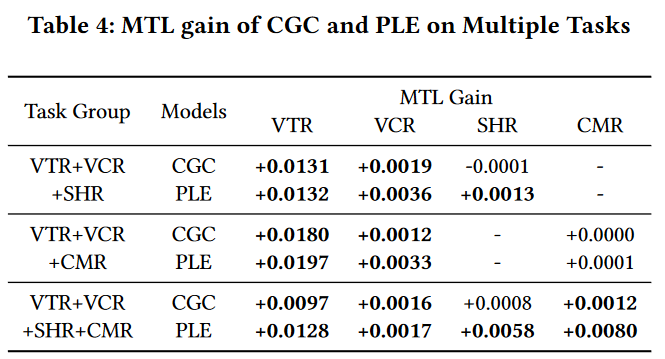
除了VTR和VCR,作者还做了CTR和VCR的实验,以及更多任务的实验,从表4的实验结果上看,似乎同一个任务数量,不同的任务组合也是有明显差异的,作者没有在这里具体分析
个人总结
是很有insight的研究,分析对比了很多方法,并进行了分类整理,图1是非常具有条理性的。
提出的方法在多任务上具有很强的泛化性,可以被后续的研究所利用,例如Hinet中就有使用。
除了私有的数据集,还进行了公开数据的很多实验,可以被很好的复现。