Improving Training Stability for Multitask Ranking Models in Recommender Systems
Google 2023 KDD | 解决多任务下精排模型的训练稳定性问题
解决多任务下精排模型的训练稳定性问题
贡献点
- 通过实验讨论了精排模型训练的不稳定因素(从模型角度和训练的角度)
- 基于训练过程中的动态变化,解释了不稳定的原因
- 提出一个算法用于缓解模型训练的稳定性问题
背景介绍
训练时的不稳定问题
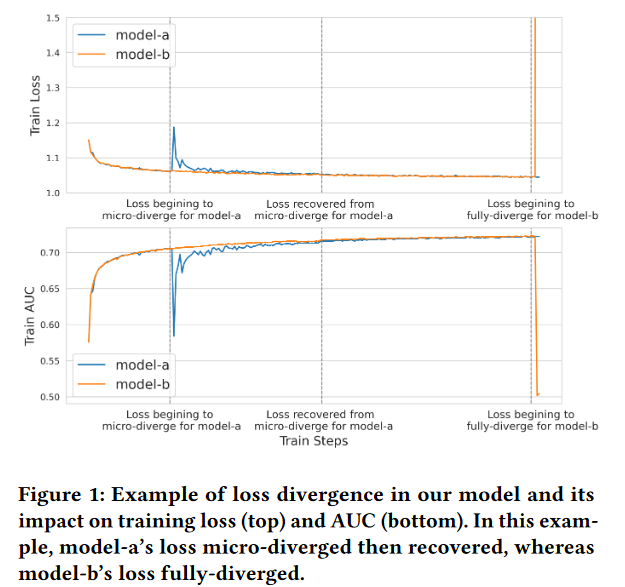
作者将训练时的不稳定症状称之为”损失发散 (loss divergence)”,分为两种类型:
1) micro-divergence : 损失曲线波动明显,但最终能够收敛,不影响最终的效果,如图一中的蓝色曲线
2) full divergence : 随时的曲线再最后变得非常大,最终模型不可用,如图一的橙色曲线
已有的训练稳定性研究
作者列举了几种常用的解决稳定性的方法,在实践中确实是经常使用的
激活层翻转
梯度剪裁
学习率warm up (如
AdaSparse中使用了递增的正则化系数,也是同样的思路
)
正则化策略 (如PLE在面对多任务时,引入了多任务归一化)
但是作者发现,这些解决方案并不能够解决他们的模型在训练中的稳定性问题(之后通过实验论证)。
他们的模型?
具体而言,作者认为他们的模型(Youtube的视频推荐精排模型Recommending what video to watch next: a multitask ranking system)是具有代表性的,具有如下几个特点
- 多任务
- 持续的训练:即模型是基于老版本的模型在新的数据上进行训练的(实时根据用户的行为进行参数更新),导致数据的分布可能发生很大改变
- 基于大Batch的训练:用更大的Batch更大的学习率加速学习,并且更小的噪声,但这样导致了训练的不稳定
训练稳定性的根本原因与case studies
根本的原因是梯度下降的步长过大,且同时损失曲率也很大,即当解在比较陡峭的损失平面的时候,迈了一大步。
RQ1: 为什么推荐系统的训练稳定性更差?
- 相较于其它任务,推荐系统的输入维度更大(童话参观大几个数量级)
- 在持续的学习中,数据的分布可能会改变,当分布发生变化,训练的损失平面会更加陡峭
- 为了学习的效率,采用大Batch、更大学习率的学习设置
RQ2: 为什么通常排序模型会比召回模型更容易出现训练稳定性问题?
- 排序模型有更大的模型大小和复杂度
- 排序模型的优化目标通常比较多,例如多目标优化、剪枝正则等等,但是召回模型的目标可能只有二分类的交叉熵,而且排序模型可能是多任务的,某一个任务产生的异常梯度会反向传播到整个(shared)模型
改善训练稳定性的方法(比较已有方法、提出新方法)
作者首先进行了利用梯度剪裁Gradient Clipping和自适应梯度剪裁Adaptive Gradient Clipping两种方法,都是通过阈值的超参数 $\lambda$ 控制梯度 $g$ 的大小,通常采用L2范数
梯度剪裁GC的主要思想:当梯度超过某个阈值时,梯度会进行clip操作,具体而言进行范数的归一化,可以表示为:
\[g\to\left\{\begin{array}{ll}\lambda\frac{g}{\|g\|}&\quad\mathrm{if} \|g\|\geq\lambda,\\g&\quad\mathrm{else.}\end{array}\right.\]自适应的梯度剪裁AGC基于”梯度范数的比和模型参数范数的比不应该太大”,可以表示为:
\[\left.g\to\left\{\begin{array}{ll}\lambda\frac{\|w\|}{\|g\|}g&\mathrm{if}\frac{\|g\|}{\|w\|}\geq\lambda,\\g&\mathrm{else} .\end{array}\right.\right.\]作者提出的Clippy方法
Clippy方法本质上就是: AGC+Adagrad
Adagrad是一种优化器,公式表达如下:
\[G_{t}=G_{t-1}+g_{t}^{2},\\r_{t}=g_{t}\cdot G_{t}^{-1/2},\\w_{t+1}=w_{t}-\eta_{t}\cdot r_{t},\]其中 $\eta_{t}$ 是在第 $t$ 步时的学习率 , $g_{t}$ 是此时的梯度,而 $G_t$ 是一个加速器,初始值为0.1,而使用Clippy方法希望控制如下的条件:
\[\left\|\frac{r_t}{w_t}\right\|_\infty<\lambda,\]相比GC和AGC,其实就是这个梯度的判断条件不同。首先为了增加这个系数的敏感程度,改为L无穷范数,其次,通过AdaGrad的公式可以看出,直接对模型进行修改的量是 $r$ ,所以为了更好的捕获模型参数的改变,所用的系数也发生了改变
论证Clipy的有效性
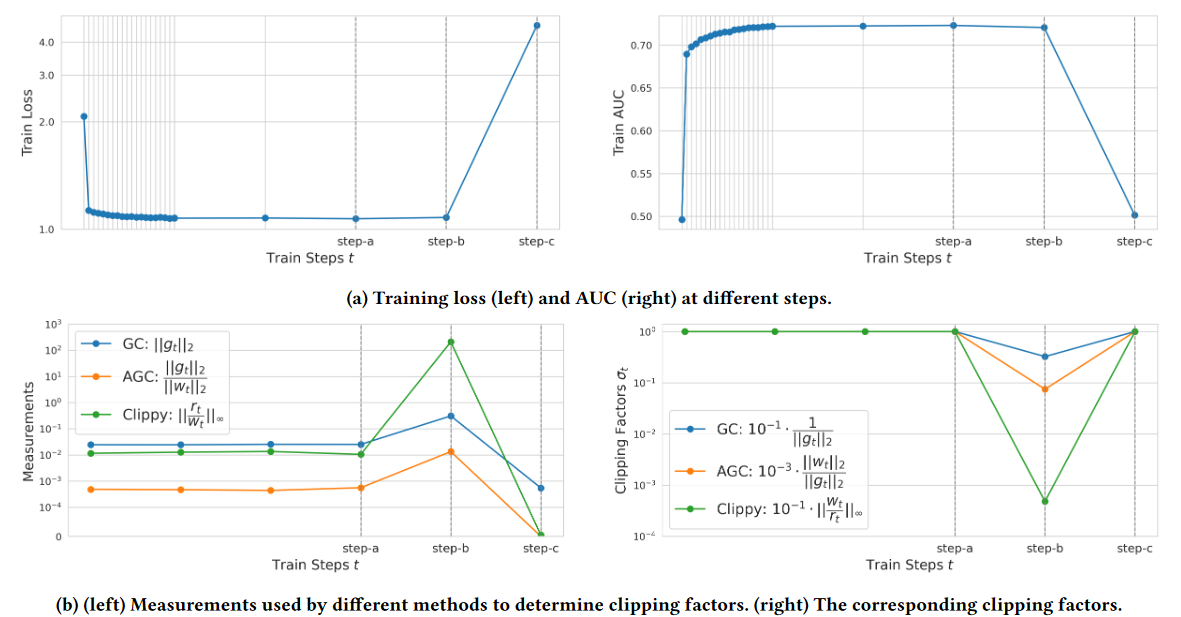
作者通过一个没有做任何稳定性控制的训练过程来论证方法的有效性,实验结果如图4
图a表示训练时的损失和AUC表现,可以看出在step-b出现了损失发散的倾向,而最终在step-c点完全发散,导致模型不可用。
图b的左图可以看出来,三种方法在异常的step-b点会增长,说明此时的损失曲面很陡峭,Clippy的增长最大,体现Clippy更加敏感的捕获损失曲率陡峭的时刻
而图b的有图是对梯度的剪裁,此时Clippy的剪裁系数是最小的,这个系数其实就是剪裁条件的倒数,那么这个系数越小,说明控制的数值越大,那么越容易超过阈值,由此可以看出Clipy对于剪裁的判断也是最敏感的
作者最终提出的算法如下伪代码
如何理解第八行?
针对Clippy的约束条件 \(\left\|\frac{r_t}{w_t}\right\|_\infty<\lambda\) ,可以转换为 $g\to\sigma\cdot g,\mathrm{~where~}\sigma=\min{\left|\frac{w_t}{r_t}\right|_{\infty},1.0}$ ,作者在此基础上另外的变化有:
增加了两个超参数变为伪代码中的 \(\frac{\lambda_{\mathrm{rel}}|w_{t}|+\lambda_{\mathrm{abs}}}{\eta_{t}*|r_{t}|}\) ,分别是绝对阈值 $\lambda_{abs}$ 和相对阈值$\lambda_{rel}$,通过绝对阈值防止模型参数为很小时的剪裁,相对阈值其实就是普通的阈值。
当模型的权重近似为0时,Clippy变为了GC
$\lambda_{\mathrm{rel}}|w_{t}|$ 远大于绝对阈值时,Clippy变为了AGC
再分母增加了学习率,当学习率很小时,阈值很大,即不容易剪裁,其实是为了加速学习
实验部分
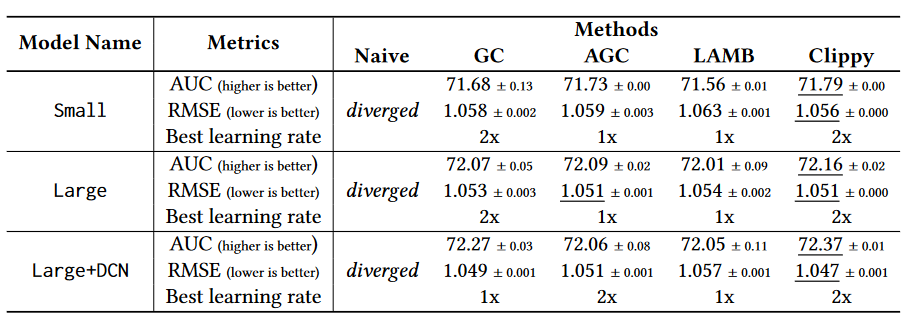
作者尝试了三种不同的模型,基于不同的模型大小和结构,结果如下表。最后的结论可以总结为:收敛得又稳定(AUC和RMSE高)又快(2x的学习率)
个人总结
解决了实际的模型训练问题,结合了Adagrad提出了Cliipy,其实就是一种剪枝方案。
非常明显的不足之处:
- 例如学习率热身等等方法,作者只是通过实验说明了不有效,但是没有讨论为什么其它人用是有效的
- 实验与讨论主要基于他们的模型,没有考虑更多的模型架构
- Clippy本质上还是通过作者的模型,在训练时的表现观察得到,不知道泛化性怎么样