AdaTT: Adaptive Task-to-Task Fusion Network for Multitask Learning in Recommendations

Task-to-Task的融合策略实现多任务学习

Task-to-Task?

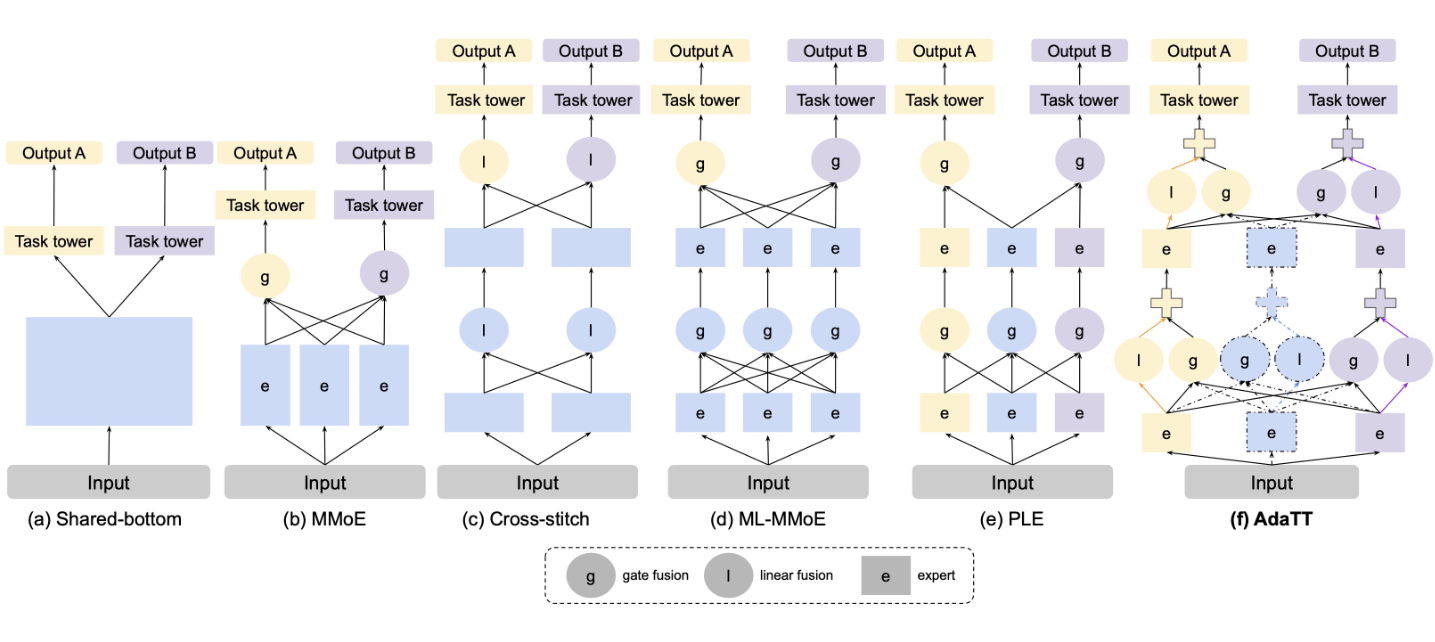
其实通过下图(Figure 2) 的对比可以明显的看出什么叫Task-to-Task。

如作者在Related work中所说，“PLE is the most relevant to ours”。仔细看图2，PLE是有task-specific的网络连接方式，多个不同的任务之间通过中间的shared model进行语义融合

而Task-to-Task直接将不同任务下的专家模型输入到task-specific单元中

作者是这么比较他们的工作与PLE的:

Differently, our work introduces two kinds of complementary fusion modules to separately model task-specific learning and shared learning. Also, in addition to explicitly introducing shared modules for learning commonalities across all tasks, we leverage direct task-pair fusion, based on the input, to maximize the flexibility of knowledge sharing.

重点在于

• 两种互补的 (complementary)融合单元去分离任务特定和共享的语义学习
• 直接采用任务对 (task-pair) 融合 （即Task-to-Task)

---

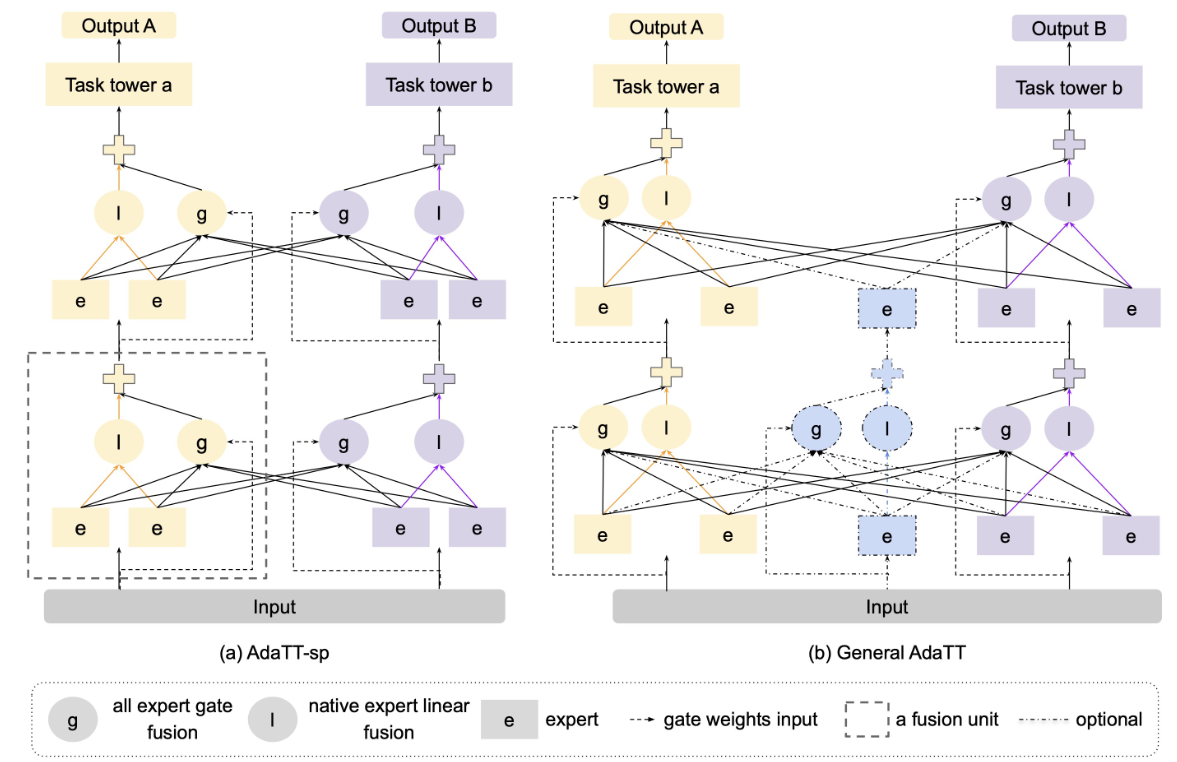
AdaTT-sp

为AdaTT的special case，即没有考虑shared model时的例子，Ada代表Adaptive，其就是就是每个Task的权重是通过模型确定的、自适应的，而不是pre-defined，其实换成learnable也是一样的

将AdaTT-sp进行公式化表示:

结合上图 (Figure 1)， 对于输入为 $x$ ，任务总共有 $T$ 种，$y_t$ 代表任务 $t$ 的输出，即 $y_t=h_t(f_t^L(x))$

AdaTT同样也是层次化的，可以认为有L层堆叠而成，上图其实就是一个两层的结构。所以对于任务t的塔 $h_t$ 其输入为第L层的模型输出 $f_t^L(x)$ ，这里的x代表的是上一层的输出，如果是第一层，才是输入的用户特征、物品特征等数据

e其实是专家系统，在横向对比的Figure2中不同，Figure1中画了两个e，其实这里的两个e就是Figure1中的一个e，这里的e代表的其实是专家系统中的“专家”，即集成网络中的一个网络，这里认为一个专家系统中有2个网络，那么对于第i个网络，公式表达为

\[E_{t,i}^l=e_{t,i}^l(f_t^{l-1}(x)),\]

$E_t^l$ 代表任务 t 在当前层 l 的输出，$E^l$ 代表当前层所有任务的输出，即

\[E_{t}^{l}=[E_{t,1}^{l},E_{t,2}^{l},\ldots,E_{t,m_{t}}^{l}],\\E^{l}=[E_{1}^{l},E_{2}^{l},\ldots,E_{T}^{l}],\]

---

legend中 I 和 g 的公式表示

I 代表线性层，输入只有当前任务 $E_t^l$ , $v_t^l$ 代表当前任务、当前层模型 I 的权重，则有

\[NativeExpertLF_t^l(E_t^l)=v_t^{lT}E_t^l,\]

G代表门单元，输入为当前层所有模型的输出 $E^l$

\[AllExpertGF_t^l(E^l,G_t^l)=G_t^{lT}E^l,\]

$G_t^l$ 代表模型单元的输出，不是权重，这里其实在做内积的特征融合，G是一个模型，其输入为前一层的输出，这就是Figure 1中 虚线箭头 gate weights input的含义，即门的输入其实为input，实线箭头知识代表门单元融合，这里的图有一些误导人， $G_t^l$ 可以由简单的权重为W的MLP通过下式得到：

\[g_t^l(f_t^{l-1}(x))=softmax(W_t^lf_t^{l-1}(x)^\intercal).\]

最后，得到 l 层的输出

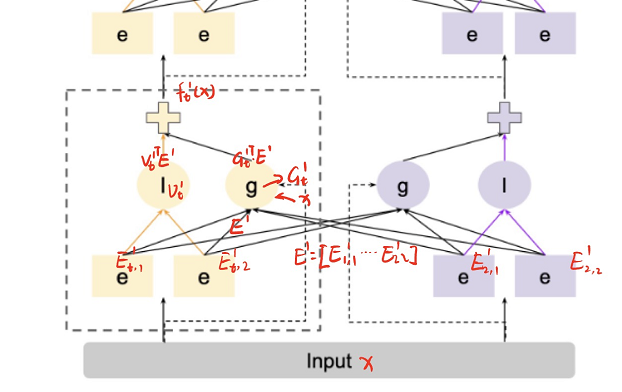
\[f_t^l(x)=AllExpertGF_t^l(E^l,G_t^l)+NativeExpertLF_t^l(E_t^l),--\]

---

如果将公式加入到Figure 1中，会更好理解：

---

对于AdaTT，就是增加了一个shared model，共享模型的专家系统的输入也一并到 $E^l$ 之中

---

实验

实验设置

超参数: 对于对比方法的MMoE和PLE，都同Figure 2，采用两层的结构，分别网络采用256和128维的单层感知机。所有的门单元都是用一层感知机，用softmax作为激活函数。所有的塔都是64维度的单层感知机。

---

Metric and Task

作者评估了两种类型的任务：consumption and engagement tasks

Consumption tasks： 理解为用户的操作，例如短视频平台中的购买、点击、观看

Engagement task: 理解为用户与平台的互动，例如主动的搜索、评分、分享 (感觉就是更“重”的操作)

---

Metric： 这里使用了归一化熵normalized entropy进行估量，公式为 $-\frac{\sum_{i=1}^np_i\log(p_i)}{\log(n)}$ ，比较适用于样本不平衡的情况

---

主要实验结果

作者在单一任务上，和多任务上都进行了比较，实验结果现实能够SOTA，并且涨点也很多。在公开数据集(UCI Census income dataset) 可以提高0.1%左右，很高。

消融实验与分析

without NativeExpertLF，即没有 I 模块，直接将 g 的内积与专家系统进行拼接作为下一层模型的输入，去掉该模块让NE增长了0.107%~0.222%

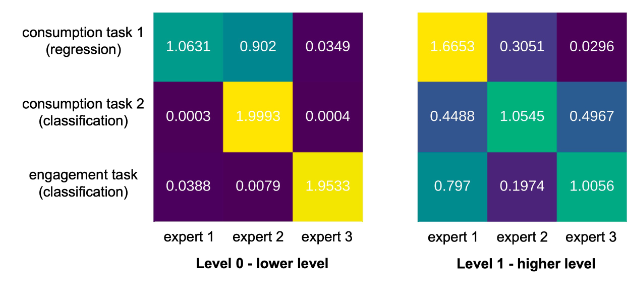
不同任务的专家可视化结果：

每个专家只使用了单个网络，作者给出的分析：在底层网络会区分不同任务的关系，而在高层会联系起各个任务。

体现论文Introduction “multiple levels of fusion, each specialized for different functionality“

---

个人总结

和PLE的工作很类似，都是由任务特定和共享的专家系统组成，但不同之处是Task-to-Task的特征融合，而不是PLE中Task-Shared融合。作者说的互补的融合单元，就是I和G的结构，一个用于进行专家的融合一个用于任务之间的融合。

从实验上看，论文的涨点效果非常明显，基本可以提高0.1%的NE